ge·o·me·tri·a
(grego geometría, -as)
substantivo feminino
1. Ciência que tem por objeto as dimensões das linhas, das superfícies e dos volumes.
2. Tratado sobre essa ciência.
"geometria", in Dicionário Priberam da Língua Portuguesa.
GEOMETRIA ESPACIAL
Há aproximadamente 1.850 a.C, a geometria espacial é originalizada, particularmente no Egito, através de estudos gravados em seus papiros, e entre seus diversos, os mais relevantes são ''Papiro de Rhind'', que apresenta 85 óbices e ''Papiro de Moscou'', que apresenta 25, todos pendentes de resoluções extraídas da geometria espacial e aritmética.
Na geometria espacial existem conceitos diversificados que adjuntos formam as principais características da ciência em questão. A primeira delas é a forma como ela trabalha, sublevando as figuras planas à três dimensões: altura, largura e comprimento, facilitando a aplicação de cálculos para diversas finalidades em determinadas áreas, como por exemplo, a engenharia, arquitetura, astronomia e entre outros.
Nesse post em questão, eu falarei um pouco sobre os corpos redondos e poliedros, suas características e suas relações básicas. Mas antes disso, vamos entender alguns termos presentes nas informações que virão em frente.
As arestas são linhas conectadas entre si que unem as faces de uma figura geométrica. Como na ilustração abaixo, cada uma dessas linhas, inclusive as posteriores, são levadas em conta. Seguindo essa lógica, o cubo possui 12 arestas.

As vértices são o ponto de encontro de todas as arestas. Seguindo essa lógica, ao final de todas as arestas, existe uma vértice, que geralmente aparece com um círculo como sinalização. Veja o exemplo abaixo, em um pentaedro e suas 6 vértices.
As faces são as superfícies exibidas, levamos em conta também a base e o topo. Nessa lógica, o cubo na ilustração possui 6 faces.
Convexo é uma característica presente em figuras geométricas onde suas vértices e arestas são exteriorizadas, como a imagem abaixo apresenta.
Um polígono não convexo é aquele que possui suas arestas interiorizadas, de forma acentuada ou não, como mostra a imagem abaixo.
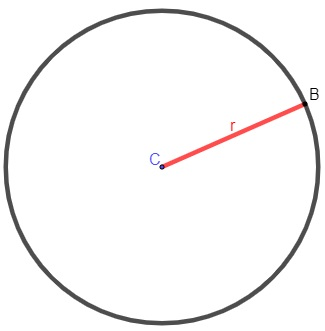
O raio é a metade de um diâmetro em sua circunferência, ou seja, encontra-se centralizado no poliedro.
Diâmetro é a maior medida que existe no centro interno de um círculo, ligando dois pontos de uma circunferência.
São segmentos de retas que não se cruzam, mas que se encontram e não permitem espaços entre si. A partir do momento que a figura plana tiver curvas, se cruzar ou não se encontrar, deixa de ser um polígono.
Esses são os termos básicos que serão citados nesse post. Agora que você já conhece seus respectivos significados, podemos prosseguir para os conceitos dos corpos redondos.
CORPOS REDONDOS
Esfera. Corpo redondo tridimensional, sem retas e uma única face curvilínea.
Uma das características mais notáveis é sua simetria, por se resumir sempre em uma circunferência arredondada, ela formará mais círculos caso seja partida ao meio.
A esfera possuí um conjunto de pontos com o raio igual ou menor que o centro.
O cilindro também é um corpo redondo tridimensional, formado inteiramente por dimensões em espiral, desde a base até a sua única face que contorna o próprio eixo.
Seu raio é paralelo com seu plano. Assim como a esfera, não possui lados ou vértices justo pela sua principal característica de ser arredondado.
POLIEDROS
Os poliedros são figuras geométricas, também tridimensionais, que se formam pela adjunção de polígonos regulares, onde seus ângulos estão todos em congruência. Diferente dos corpos redondos, os poliedros possuem: vértices, arestas e faces. Além disso, eles também são separados em três categorias: convexos e não convexos, também denominados de côncavos, e regulares.
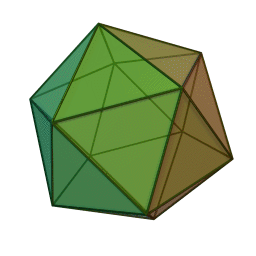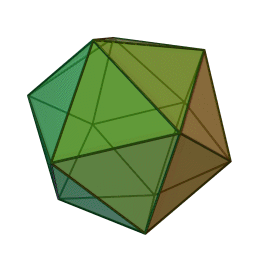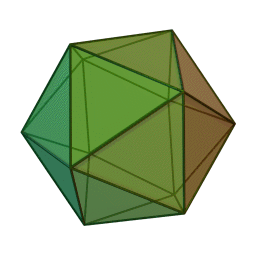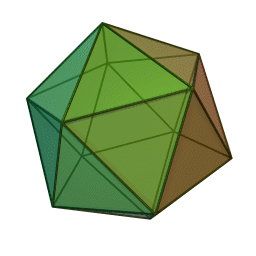
Icosaedro. Poliedro convexo, já que sua superfície se volta para o exterior, também tridimensional e, diferente dos corpos redondos, o Icosaedro possui 20 faces, 30 arestas e 12 vértices, formando um triângulo equilátero, que fora identificado pelo filósofo matemático grego Platão.
O que lhe difere dos outros poliedros platônicos é o fato de que sua inscrição é a única que se forma em torno de uma esfera.
Hexaedro. Poliedro, também convexo, tridimensional. Possui 6 faces, 12 arestas e 8 vértices, formando um cubo regula, e também pertence ao descobrimento do filósofo grego Platão.
CONCLUSÃO
A geometria espacial é mais um ramo da geometria em si, uma ciência que estuda os corpos tridimensionais, construída minuciosamente por diferentes filósofos gregos, usando pontas, superfícies e curvas para realizarem seus estudos.
É isso. Essas são todas as informações que eu consegui processar e explicar. Acho que não será necessário inserir nenhum site para complementar o que eu fiz aqui, então é só isso mesmo.
Imagens não autorais. Fonte:
Arestas, vértices e faces.










Comentários
Postar um comentário